
| Go Articles |
 | |
| Setpiece Kos |
This article was initially intended to be part of 'Secret Weapons', which will now be part 7 of the series. It grew to be long enough to stand on its own.
Introduction
Pre-numerical ideas
Basic numerical ideas
Expectation (coin-tossing)
Overall value
Tally reasoning
Models with threats
Graphical presentation of stake with threats
Worked example of a picnic ko
Eventually one can't escape the idea of a ko fight as a transaction in which trades are made, quantifiable if not exactly so, and by a tricky mechanism: ko as an arcane financial instrument, perhaps. The point of theoretical discussion is then to pin down the idea that there is a calculable, correct return on fighting a ko: what we shall later call its honest value. It is quite an effort to disentangle this idea in the many possible approaches. Naturally the idea that ko fights are simply a gamble isn't good enough. It does give one clue: try to analyse what is at stake in the fight.
This is a good idea, because an accurate reckoning of 'the stakes' in a ko fight represents half the battle. Our procedure is to analyse here, in quite some detail, the way of accounting for a ko, at least in the stop-loss case (winning the ko for either side is something to which one can give a numerical value) - this might not be right where one side's position then disintegrates, but that is sufficiently like an all-dominating ko (see section 4 below). This may seem like quite hard work, but ko doesn't give up its secrets too easily. One should note that in typical middlegame positions a ko may be fought, for example, over the eye space of a weak group; in which case you have to apply some method for counting the value of weakness and strength. This is an area on which Rob van Zeijst has been writing (QARTS).
The other half of the reckoning of the 'honest value' is to weigh up the supply of ko threats. We shall look at this later by means of the 'gaps and overlaps' analysis (Tavernier's method) - also under quite heavy modelling assumptions. The basic idea can be found in section 6.
This is a preliminary section. The only way to get a good theory of ko is to assume both sides are competing for an objective that is numerical (can be expressed as gain or loss of a definite number of points); and that both players choose the best possible line of play. What is said here covers all other cases.
The factors in the section title are important in general in playing go at amateur level; and especially important in relation to ko fights. They aren't really aspects of the game corresponding to proper theories, but are rather obviously part of the arsenal of the games-player who aims to win. They are mentioned here because of their practical significance. A player may well start a ko for any of these reasons:
Equally a player may
Although side-bets on a game of go are hardly unknown, the game itself involves no chance element. And that statement ought to cover ko fights as much as anything else.
It can of course seem that the need to find ko threats during serious ko fights introduces a random element into an orderly and peaceful game. That point of view certainly misses something about go as a game of complete information; the supply of ko threats for each side is in plain view for both players.
An expression like 'raising the stakes', as applied to the deliberate starting of a large ko fight in which either side may take a major loss, does reflect something about practical strategy. Such a fight may seem to be the only real chance of winning a game from a poor position judged by secure territory; the way the ko threats match up for the two players as the ko is played out will reveal much about whether the position was as one-sided as appeared. Certainly in the most complex cases the overall position can be transformed, without clear mistakes being made.
You really must count something during a serious ko fight, if only to check that the overall position is so one-sided that you can ignore any threat. Global counting of the game is required for intelligent play.
When introducing actual numbers into discussions of localised sequences, one has to get straight the possible scale or counting conventions. This can't be done without a little careful thought. You can skip the rest of this section, or read another treatment (deiri counting, miai counting), if it turns out that you don't like my style of explanation.
There are actually three concepts one needs, related in such a way that one can define the third in terms of the other two. Local tallies were brought in as Concept A. So-called deiri or swing counting can serve as the second. Exhibit a local situation S, with rival outcomes after Black and White plays; and count the points difference that makes as best one can.
That is, we have to hold in our mind two positions, corresponding in tally to SB... and SW... with a few stones added, and differing in value to the players by a measurable amount, called the swing, or traditionally the deiri count. We can make the definition
miai count x tally difference = deiri count.
Therefore, as long as the tally difference isn't zero, the miai count is deiri count/tally difference and represents how hard the added stones work in the comparison of positions. The miai count is the number telling us per play how much Black or White gain by investing in this part of the board. This is valuable information if it is available, even approximately.
Miai counting for straightforward gote plays comes to comparing SB and SW results (Black takes gote, versus White takes gote) and dividing the swing made by the tally difference, two. Therefore what is ordinarily called a 12-point gote endgame move is also properly treated as a six-point play, miai counting. It is miai scores that compare directly, and we draw the consequences for ko under 5 below.
One-sided sente plays correspond in this equation to tally difference equal to one: if an endgame play is Black's one-side sente, you should compare positions starting from S which are like SBWBW...BW with positions SW in which White prevents Black carrying out the sente continuation. The tally difference is therefore one play by White. So, for one-sided sente plays, no need to state the convention used. For double sente plays, the miai value isn't computable because the tally difference is zero. Those correspond in practice to urgent and volatile situations that both players covet.
Pedantic note about scoring method: Chinese-style (area) scoring will give miai counts that are consistently higher by one than Japanese-style (territory) scoring. Evidently that makes no difference when miai counts are compared to see which is larger. Deiri counts will change therefore according to the tally difference. Unless a ko is of small value or a very precise count is required, it is safe enough to disregard differences between methods. Of course if you insist on exactness you must specify a method.
Algebraic formulae such as we shall using are safe (dimensionless, you could say). The traditional names 'deiri counting' and 'miai counting' are often found unintuitive, not least by this author.
We assume from now on that capturing and then finishing the ko with one further play leads to a gain of a points for Black, and to a gain of b points for White. Taking Black's point of view, a gain of b for White is the same as a loss of -b for Black. If we have no further information on the state of threats or the fight, we assume that either side has an equal chance to win the ko (the same as tossing a fair coin to see who wins). Black's expected gain from the ko is then (a-b)/2.
The main use of this model is in case one of a and b is much larger than the other. This is the type of ko called 'picnic ko' (Japanese hanamiko). If say a is much larger than b, White stands to lose much more than Black. Unless White has a preponderance of large ko threats, White may be forced to finish the ko early. Black may not need to play this ko for its full value (what we shall later call the honest value), simply taking enough profit to turn the overall game position to favourable. Therefore the term picnic ko might be taken to refer to one side's informed decision that limited profits from a ko fight are enough: that is, it describes one form of the relaxation mentioned in section 1. It may of course also refer to the other side's decision that the ko is unfightable, requiring some earlier concession to be made.
With the same notation, there are a+b points at stake in the ko. In some cases this swing will be enough to decide the game. For example, it may be 100 points, and killing a group of normal size elsewhere on the board may only be worth 50 points. This is the type of ko known as 'all-dominating'. The only threats that matter in such a ko are local threats. Absent local threats, the first player to capture the ko will win it, by ignoring the opponent's next play.
In order to get further insight one has to move from simple probabilistic models, which were known in the seventeenth century to Pascal, towards the game theory of the twentieth century.
If we look at the local tally in the ko position K, how does it vary between the outcomes? Assuming Black is the first to capture the ko, and wins it with one further play, the tally becomes KBB. If on the other hand White wins it the tally will be KW. Because by convention we cancel BW away, there is no need to take into account the various times the ko is fought by taking and retaking.
Therefore the two tallies differ by three plays (KW + BBB = KBB). The total value model ought to be qualified by saying that a+b points is gained but the opponent has three net plays to match that.
Sente may change hands in the ko fight: if Black starts the fight but loses the ko, White will emerge with sente after Black follows up the ignored threat.
It is miai values that compare directly. For example a ko might be described by deiri or swing count 18 = a+b as its total value, comparing postions tally three apart (as we just saw). It can reasonably be thought as urgent to play in as the 12-point gote endgame position mentioned in point 2: they each have miai value 6.
Tally principles reconsidered:
In part 2 of this series the Addition Tally and Subtraction Tally Principles were introduced. These rules can no doubt be replaced by detailed consideration of processes of tally addition in ko (which might raise the tally change to four or five net plays) going on in parallel with ko enlargement (increases in the swing count of the ko).
Changes of both kinds have an impact on the miai value of plays in the ko, but in opposite directions. What one means by enlarging the ko is to add to the deiri value. This is done by ignoring a ko threat and playing an extra stone in the region of the ko. Therefore the tally also rises. Looking at the effect on
miai count= deiri count/local tally difference
one is asked to compare two fractions. The miai count goes up when the deiri count rises by a larger proportion than the tally.
Therefore one can't simply accept the Addition Tally Principle, for example. That suggests that the player enlarging the ko finds it more urgent to win it. But there is a quantitative story that needs to be told about it, too. Still, if we assume that the player enlarging the ko does it to make the ko more urgent, i.e. to increase the miai value, this makes sense.
Note on the other hand that if you add a play to the ko, it becomes easier for your opponent to treat it as a picnic ko, because of the profit taken by one play elsewhere in the overall scheme of things. That says that the Subtraction Tally Principle, apparently converse to the Addition principle, really comments on relaxation.
To summarise this discussion, you have to know when to press for extra profit from the ko, by enlarging, when to back down by diminishing the ko's (deiri) value, and when to relax and take profit elsewhere instead of being stubborn about the ko. Seong-june Kim's favourite saying about all this is "be the bullfighter, not the bull". There are two kinds of basic mistake:
We assume that the players can foresee enough about the ko to predict the outcome as a choice: Black gains a points by ignoring a white threat of value c; or White gains b points by ignoring a black threat of value d. The threats should be set against the gains, in both cases, so Black takes a-c, or White takes b-d. Black's payoff is therefore a-c or d-b.
These numbers may be positive or negative. Naturally if Black starts the fight it is in the hope of putting White on the horns of a dilemma: lose a points with a threat of value c, or gain b points ignoring a threat of value d? Black starts the ko in cases where both a-c and d-b will be substantial and positive - possibly making allowance for a number of major threats for both sides being matched off first.
The difference (a-c) - (d-b) is (a+b) - (c+d), so that the total value a+b is set off against the combined value c+d of Black's and White's threats. Black will gain by ignoring White's threat of value c, in comparison to White's ignoring Black's threat of value d, only at that stage in the ko fight where c+d has dropped below a+b in value. This matter can be developed into a proper minimax criterion for best play, which was mentioned in the introduction above, and to which we shall return later in this series (Tavernier's model).

The graphical representation of the algebra here turns out to be a big help, conceptually. White's threats are drawn as lines down from a horizontal line, and Black's threats up from another parallel line. The distance between the lines should be the stake a+b. Then in case c+d > a+b the difference between the two represents the overlap of the lines in the picture. If c+d < a+b there will be a gap of size the difference. The appearance of such a gap during the ko fight is the sign that a player should ignore a threat.
The previous model of section 6 is flawed in that it takes no account of the possible transfer of sente that was mentioned under the tally model in section 5; one ought to combine the good features of both. To move in that direction, we imagine that the player starting the ko - Black as we have been discussing it - adds to the stake a 'marker' representing the possession of sente. If Black wins the ko fight and retains sente, Black picks up the marker again. But if White wins ths ko and takes sente, as Black carries out the threat that has been ignored, White picks up the marker. Black must redeem it by paying an amount m. This is an imaginary transaction we add into the picture for book-keeping purposes.
With this understanding the formulae from the previous model become Black payoffs a-c or d-m-b. The difference formula becomes (a+b) - (c+d-m), reflecting the extra incentive White, the second player, has to win the ko and take sente. The graphical model shown under 6 adapts easily: we should write this formula as (a+b+m) - (c+d), and then this is just as before, with the stake a+b replaced now by a+b+m.
To quantify this, suppose for example the ko fight is the last big event of the middlegame. Then m represents the value of the right to start the endgame. In normal circumstances this is worth something like 10 points (see comments in section 2 about conventions: this corresponds to saying the largest gote endgame points are about 20 points deiri, and that the possibilities for double sente and reverse sente plays don't add significantly). Sometimes it would be worth more.
A different way of looking at the problem is interesting, not least because it gives a handle on the value of 'markers'. In the absence of substantial threats, or assuming the main threats for the two sides effectively cancel off, the supply of interesting threats comes down to 'the environment': the remaining big points, of typical value e say. For example, these might be large gote endgame plays.
Their effect when played in the ko is like ko threats of value 2e: you play a gote move of size e as a 'threat', without expectation of any local answer to it, and then another one as follow-up. This makes the na´ve ko threat model have payoffs a-2e, 2e-b for Black, so that the significant difference becomes (a+b) - 4e. That's certainly wrong, since the tally difference is three not four. The marker model gives (a+b) - 4e + m. The suggestion is that m = e; nothing else adds up.
That would reduce the comparison to a trade of a+b versus 3e. Now the factor matches the tally count. The total gain in the ko, a swing of a+b, represents a tally difference of three plays. The break-even between playing in the ko and playing in the environment should occur when (a+b)/3 = e.
That is, we look at the miai count of plays in the ko. When that value is precisely equal to the background value e of typical plays in the rest of the game, the ko is ripe to be played for its own sake. The value of plays in the environment tends gradually to decrease. We have identified the cross-over point, at which it is worth fighting the ko, without the synergy effect of getting two plays in a row somewhere coming into the calculation. This kind of reasoning is typical of endgame positions. When the best anyone can do with sente is to make plays of miai value e, you can discard the marker concept.
The same conclusion comes from the analysis of Black's behaviour on losing this sort of ko fight: when Black starts the ko, White first ignores a Black play (worth e to recapture), and a second such play of value e to finish the ko, Black can take simply take sente (pick up the marker) rather than 'follow-up' the 'threat'.
It is also well worth checking what happens here in the graphical model introduced in section 6. The ko threats have value 2e - the environment assumption is that all threats have this value, and that there are an indefinite number of them. According to section 7 the 'stake' - distance between the parallel lines - should be set at a+b+e. The case a+b=3e is exactly the critical case where a small overlap turns into a small gap.

This view of the 'stakes' is the one adopted by Simon Goss in a recent series of British Go Journal articles that are being posted here, though it appears we may have to be patient in waiting for them.

This is a position from a real game (Chinese prodigy Liao Xingwen versus past European Champion Lee Hyuk, on four stones). Black has a method of attacking the two marked stones, but it is dangerous. Black could lose the corner when a ko arises.
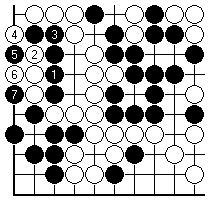
After Black 7, Black may succeed in rescuing the five-stone group inside White's territory, by capturing the four white stones on the edge that are suffering from shortage of liberties. White, however, has a ko to capture Black 7.

Here White has won a ko twice and Black's corner is dead. This is naturally a bad result for Black. What is the tally count? Compared with the starting position White has played two more stones here so it is WW.

Supposing Black wins the ko by taking the four stones. This is the result, and the tally based on the starting position is BB. Therefore the total tally difference here is four plays. That's one more than the predicted three, because White doesn't have a direct ko.
The points difference between the last two diagrams is our a+b for this position. It can be calculated by a direct count of territory and prisoners, with some harmless assumptions about further plays on the edge (this example is relatively simple as far as further follow-up plays goes). Just this once we are going to do this explicitly (territory counting)...

We make the assumption of Black A White B on the lower edge, giving White 15 points there (including the marked stones). Assume White C later. Then at the 'x' points count two for Black (a white stone has been captured there), and one elsewhere in the corner. Black also has fifteen here. We ought though to remember the throw-in stone at 5 in the second diagram, which is one extra to White.
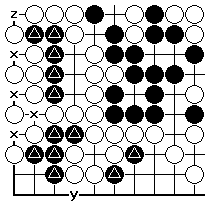
After White's victory it looks like this with the marked black stones all dead. White still has fifteen points to the right of 'y', so we just forget that whole area in determining the swing here. Counting from 'y' leftwards, including two points for each 'x' points as well as for the dead stones, and giving White a point at 'z', White now has a total of 36 points here.
Therefore the swing is 36+14=50. The miai value of plays in the ko is seen to be 12.5 (quite high, even though the ko isn't direct).
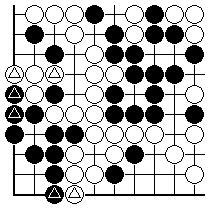
The final piece of work here is to find the starting place, i.e. recover the values of a and b individually: at present we know their sum. For that we have to visualise the ordinary endgame result here, if Black doesn't fight the ko. It shouldn't be worse for Black than this diagram.
Here White's territory on the left is 14, Black has six in the corner, making on balance White +8 (leaving out the lower side once more). Therefore Black can gain 22 in the ko, as we see by comparing with the diagram where Black has won the ko, and White 28.
Therefore although this appears on the surface to be rather clearly a picnic ko adverse to Black, that feeling isn't really supported by the figures. Black stands to lose more, but not hugely. White requires two plays to win the ko, rather than just one for Black. This ko could have been played by Black in the middle game. The fact that it wasn't tells you something about handicap go.
| Posted 6 September 2002. Copyright (c) 2002 Charles Matthews | ||
| Previous edition | Index | Next edition |